| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 1.1 | Example 1 (Before Exercise 1.2) | Exercise 1.2 |
| Example 2 to 5 (Before Exercise 1.3) | Exercise 1.3 | Example 6 & 7 (Before Exercise 1.4) |
| Exercise 1.4 | ||
Chapter 1 Integers
Welcome to the comprehensive guide detailing the solutions for Chapter 1: Integers, a pivotal chapter that significantly expands upon the foundational understanding developed in Class 6. While earlier studies introduced the concept of integers (positive whole numbers, negative whole numbers, and zero), their representation on the number line, and basic addition/subtraction, this chapter dives much deeper. Here, the focus shifts towards mastering the operations of multiplication and division involving integers and formally exploring the fundamental properties that govern these operations. A solid grasp of integers is absolutely essential, as they form the numerical bedrock for virtually all algebraic concepts encountered later in mathematics.
The provided solutions meticulously guide students through the intricacies of integer arithmetic. A primary area of focus is the multiplication and division of integers, paying close attention to the crucial sign rules:
- Multiplication:
- Positive $\times$ Positive = Positive ($(+) \times (+) = +$)
- Negative $\times$ Negative = Positive ($(-) \times (-) = +$)
- Positive $\times$ Negative = Negative ($(+) \times (-) = -$)
- Negative $\times$ Positive = Negative ($(-) \times (+) = -$)
- Division: The rules mirror multiplication.
- Positive $\div$ Positive = Positive ($(+) \div (+) = +$)
- Negative $\div$ Negative = Positive ($(-) \div (-) = +$)
- Positive $\div$ Negative = Negative ($(+) \div (-) = -$)
- Negative $\div$ Positive = Negative ($(-) \div (+) = -$)
Numerous examples involving the product and quotient of two or more integers are solved with clear, step-by-step procedures in the solutions, ensuring students can confidently apply these sign conventions.
Beyond basic computation, the solutions thoroughly explore the properties of integers under the four fundamental operations. Understanding these properties is not just about memorization; it's about recognizing patterns and structures within the number system that can significantly simplify calculations. Key properties covered include:
- Closure Property: Are integers closed under addition, subtraction, multiplication, division? (e.g., Is $a+b$ always an integer if $a, b$ are integers? Yes. Is $a \div b$ always an integer? No, e.g., $5 \div 2$ is not an integer).
- Commutativity: Does order matter? (Is $a+b = b+a$? Yes. Is $a-b = b-a$? No. Is $a \times b = b \times a$? Yes. Is $a \div b = b \div a$? No).
- Associativity: Does grouping matter for three or more integers? (Is $(a+b)+c = a+(b+c)$? Yes. Is $(a \times b) \times c = a \times (b \times c)$? Yes).
- Identities: Existence of an Additive Identity (0, since $a+0 = 0+a = a$) and a Multiplicative Identity (1, since $a \times 1 = 1 \times a = a$).
- Additive Inverse: For every integer $a$, there exists an integer $-a$ such that $a + (-a) = 0$.
- Distributive Property: The critical link between multiplication and addition/subtraction: $a \times (b + c) = (a \times b) + (a \times c)$ and $a \times (b - c) = (a \times b) - (a \times c)$.
The solutions effectively demonstrate not only how to verify these properties but, more crucially, how to leverage them strategically. For instance, calculating $(-49) \times 18$ might be simplified using distribution as $(-49) \times (20 - 2) \ $$ = (-49 \times 20) \ $$ - (-49 \times 2) = -980 - (-98) \ $$ = -980 + 98 = -882$. Associativity helps in rearranging multiplications like $(-5) \times 17 \times (-2)$ to $( (-5) \times (-2) ) \times 17 \ $$ = 10 \times 17 \ $$ = 170$.
Division specifics, including the vital concept that division by zero is undefined (expressions like $\frac{a}{0}$ have no meaning), are clearly addressed. Furthermore, the solutions tackle a variety of word problems, translating real-world scenarios into the language of integers. These problems often involve contexts like temperature changes (drops represented by negative values, rises by positive), scores in tests (e.g., +3 for correct, -1 for incorrect), changes in elevation relative to sea level, or financial gains and losses. The systematic breakdown of these problems in the solutions helps students develop logical reasoning alongside computational fluency.
Mastering the content clarified by these Chapter 1 solutions is paramount. It reinforces number sense, solidifies procedural skills with all four basic operations on integers, and instills an understanding of their governing properties, thereby laying an indispensable foundation for success in algebra and beyond.
Exercise 1.1
Question 1. Following number line shows the temperature in degree celsius (°C) at different places on a particular day.

(a) Observe this number line and write the temperature of the places marked on it.
(b) What is the temperature difference between the hottest and the coldest places among the above?
(c) What is the temperature difference between Lahulspiti and Srinagar?
(d) Can we say temperature of Srinagar and Shimla taken together is less than the temperature at Shimla? Is it also less than the temperature at Srinagar?
Answer:
(a) Observing the number line, we can find the temperature of each place:
Temperature of Lahulspiti is $-8^\circ\text{C}$.
Temperature of Srinagar is $-2^\circ\text{C}$.
Temperature of Shimla is $5^\circ\text{C}$.
Temperature of Ooty is $14^\circ\text{C}$.
Temperature of Bengaluru is $22^\circ\text{C}$.
(b) The hottest place is the one with the maximum temperature, which is Bengaluru with $22^\circ\text{C}$.
The coldest place is the one with the minimum temperature, which is Lahulspiti with $-8^\circ\text{C}$.
The temperature difference between the hottest and the coldest places is:
$22^\circ\text{C} - (-8^\circ\text{C}) = 22^\circ\text{C} + 8^\circ\text{C} = 30^\circ\text{C}$.
The temperature difference is $30^\circ\text{C}$.
(c) The temperature of Lahulspiti is $-8^\circ\text{C}$.
The temperature of Srinagar is $-2^\circ\text{C}$.
The temperature difference between Lahulspiti and Srinagar is:
$-2^\circ\text{C} - (-8^\circ\text{C}) = -2^\circ\text{C} + 8^\circ\text{C} = 6^\circ\text{C}$.
Alternatively, the difference can be calculated as $|-8^\circ\text{C} - (-2^\circ\text{C})| \ $$ = |-8^\circ\text{C} + 2^\circ\text{C}| = |-6^\circ\text{C}| = 6^\circ\text{C}$.
The temperature difference is $6^\circ\text{C}$.
(d) Temperature of Srinagar and Shimla taken together:
Temperature of Srinagar $= -2^\circ\text{C}$.
Temperature of Shimla $= 5^\circ\text{C}$.
Sum of temperatures $= -2^\circ\text{C} + 5^\circ\text{C} = 3^\circ\text{C}$.
Now, we compare this sum with the temperature at Shimla:
$3^\circ\text{C} < 5^\circ\text{C}$.
So, the temperature of Srinagar and Shimla taken together is less than the temperature at Shimla.
Next, we compare the sum with the temperature at Srinagar:
$3^\circ\text{C} > -2^\circ\text{C}$.
So, the temperature of Srinagar and Shimla taken together is not less than the temperature at Srinagar.
Question 2. In a quiz, positive marks are given for correct answers and negative marks are given for incorrect answers. If Jack’s scores in five successive rounds were 25, – 5, – 10, 15 and 10, what was his total at the end?
Answer:
Jack's scores in five successive rounds are $25$, $-5$, $-10$, $15$, and $10$.
To find the total score, we need to add all the scores obtained in the rounds.
Total score $= 25 + (-5) + (-10) + 15 + 10$
Total score $= 25 - 5 - 10 + 15 + 10$
We can group the positive and negative numbers:
Total score $= (25 + 15 + 10) + (-5 - 10)$
Total score $= 50 + (-15)$
Total score $= 50 - 15$
Total score $= 35$
Thus, Jack's total score at the end is 35.
Question 3. At Srinagar temperature was – 5°C on Monday and then it dropped by 2°C on Tuesday. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by 4°C. What was the temperature on this day?
Answer:
Given that the temperature of Srinagar on Monday was $-5^\circ\text{C}$.
On Tuesday, the temperature dropped by $2^\circ\text{C}$.
This means the temperature became lower by $2^\circ\text{C}$ from Monday's temperature.
Temperature on Tuesday = Temperature on Monday - Drop in temperature
Temperature on Tuesday = $-5^\circ\text{C} - 2^\circ\text{C}$
Temperature on Tuesday = $-7^\circ\text{C}$
The temperature of Srinagar on Tuesday was $-7^\circ\text{C}$.
On Wednesday, the temperature rose by $4^\circ\text{C}$ from Tuesday's temperature.
This means the temperature became higher by $4^\circ\text{C}$ from Tuesday's temperature.
Temperature on Wednesday = Temperature on Tuesday + Rise in temperature
Temperature on Wednesday = $-7^\circ\text{C} + 4^\circ\text{C}$
Temperature on Wednesday = $-3^\circ\text{C}$
The temperature of Srinagar on Wednesday was $-3^\circ\text{C}$.
Question 4. A plane is flying at the height of 5000 m above the sea level. At a particular point, it is exactly above a submarine floating 1200 m below the sea level. What is the vertical distance between them?
Answer:
Given that the plane is flying at a height of $5000$ m above the sea level.
The submarine is floating at a depth of $1200$ m below the sea level.
To find the total vertical distance between the plane and the submarine, we consider the sea level as the zero reference point.
The distance of the plane from the sea level is $5000$ m.
The distance of the submarine from the sea level (in the downward direction) is $1200$ m.
The total vertical distance is the sum of the distance above the sea level and the distance below the sea level.
Vertical distance = Distance above sea level + Distance below sea level
Vertical distance = $5000$ m $+ 1200$ m
Vertical distance = $6200$ m
The vertical distance between the plane and the submarine is $6200$ m.
Question 5. Mohan deposits ₹ 2,000 in his bank account and withdraws ₹ 1,642 from it, the next day. If withdrawal of amount from the account is represented by a negative integer, then how will you represent the amount deposited? Find the balance in Mohan’s account after the withdrawal.
Answer:
Given that withdrawal of amount from the account is represented by a negative integer.
This means that money taken out of the account is negative.
Depositing money means putting money into the account, which is the opposite of withdrawing.
Therefore, the amount deposited into the account will be represented by a positive integer.
Amount deposited $= \textsf{₹} \ 2000$. This is represented as $+2000$.
Amount withdrawn $= \textsf{₹} \ 1642$. This is represented as $-1642$.
To find the balance in Mohan's account after the withdrawal, we add the deposited amount and the withdrawn amount (represented by integers).
Balance = Amount deposited + Amount withdrawn
Balance = $2000 + (-1642)$
Balance = $2000 - 1642$
We perform the subtraction:
$\begin{array}{cc} & 2 & 0 & 0 & 0 \\ - & 1 & 6 & 4 & 2 \\ \hline & & 3 & 5 & 8 \\ \hline \end{array}$
Balance = $358$
The balance in Mohan's account after the withdrawal is $\textsf{₹} \ 358$.
Question 6. Rita goes 20 km towards east from a point A to the point B. From B, she moves 30 km towards west along the same road. If the distance towards east is represented by a positive integer then, how will you represent the distance travelled towards west? By which integer will you represent her final position from A?

Answer:
Given that the distance travelled towards east is represented by a positive integer.
East and west are opposite directions.
Therefore, the distance travelled towards west will be represented by a negative integer.
Rita starts from point A.
She goes 20 km towards east from A to B.
Distance travelled towards east $= 20$ km, represented as $+20$.
From point B, she moves 30 km towards west.
Distance travelled towards west $= 30$ km, represented as $-30$ (since west is opposite to east).
To find her final position from A, we add the displacements in each direction from the starting point A.
Final position from A = Displacement towards east + Displacement towards west
Final position from A $= +20 + (-30)$
Final position from A $= 20 - 30$
Final position from A $= -10$ km
The final position is $-10$ km from A. The negative sign indicates that the final position is in the direction opposite to east, which is west.
Her final position from A is 10 km towards the west.
She will be represented by the integer $-10$ to show her final position from A.
Question 7. In a magic square each row, column and diagonal have the same sum. Check which of the following is a magic square.
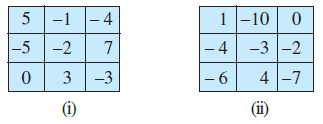
Answer:
To determine if a square is a magic square, we need to check if the sum of the numbers in each row, each column, and each of the two main diagonals is the same.
Checking Square (i)
| 5 | -1 | -4 |
| -5 | -2 | 7 |
| 0 | 3 | -3 |
Sum of Rows:
Sum of Row 1 = $5 + (-1) + (-4) = 5 - 1 - 4 = 0$
Sum of Row 2 = $-5 + (-2) + 7 = -7 + 7 = 0$
Sum of Row 3 = $0 + 3 + (-3) = 3 - 3 = 0$
Sum of Columns:
Sum of Column 1 = $5 + (-5) + 0 = 5 - 5 + 0 = 0$
Sum of Column 2 = $-1 + (-2) + 3 = -3 + 3 = 0$
Sum of Column 3 = $-4 + 7 + (-3) = -4 + 7 - 3 = 3 - 3 = 0$
Sum of Diagonals:
Sum of Diagonal 1 (top-left to bottom-right) = $5 + (-2) + (-3) \ $$ = 5 - 2 - 3 = 0$
Sum of Diagonal 2 (top-right to bottom-left) = $-4 + (-2) + 0 = -6$
Here, the sum of all rows, columns, and one diagonal is 0, but the sum of the other diagonal is -6. Since all the sums are not equal, square (i) is not a magic square.
Checking Square (ii)
| 1 | -10 | 0 |
| -4 | -3 | -2 |
| -6 | 4 | -7 |
Sum of Rows:
Sum of Row 1 = $1 + (-10) + 0 = 1 - 10 = -9$
Sum of Row 2 = $-4 + (-3) + (-2) = -4 - 3 - 2 = -9$
Sum of Row 3 = $-6 + 4 + (-7) = -2 - 7 = -9$
Sum of Columns:
Sum of Column 1 = $1 + (-4) + (-6) = 1 - 4 - 6 = -9$
Sum of Column 2 = $-10 + (-3) + 4 = -13 + 4 = -9$
Sum of Column 3 = $0 + (-2) + (-7) = -2 - 7 = -9$
Sum of Diagonals:
Sum of Diagonal 1 (top-left to bottom-right) = $1 + (-3) + (-7) \ $$ = 1 - 3 - 7 = -9$
Sum of Diagonal 2 (top-right to bottom-left) = $0 + (-3) + (-6) \ $$ = -3 - 6 = -9$
Since the sum of each row, column, and diagonal is the same (which is -9), square (ii) is a magic square.
Question 8. Verify a – (– b) = a + b for the following values of a and b.
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a = 28, b = 11
Answer:
We need to verify the equation $a - (-b) = a + b$ for the given values of $a$ and $b$ by calculating the Left Hand Side (LHS) and the Right Hand Side (RHS) for each case.
(i) Given $a = 21$ and $b = 18$.
LHS $= a - (-b) = 21 - (-18)$
LHS $= 21 + 18 = 39$
RHS $= a + b = 21 + 18 = 39$
Since LHS = RHS ($39 = 39$), the equation $a - (-b) = a + b$ is verified for $a = 21$ and $b = 18$.
(ii) Given $a = 118$ and $b = 125$.
LHS $= a - (-b) = 118 - (-125)$
LHS $= 118 + 125 = 243$
RHS $= a + b = 118 + 125 = 243$
Since LHS = RHS ($243 = 243$), the equation $a - (-b) = a + b$ is verified for $a = 118$ and $b = 125$.
(iii) Given $a = 75$ and $b = 84$.
LHS $= a - (-b) = 75 - (-84)$
LHS $= 75 + 84 = 159$
RHS $= a + b = 75 + 84 = 159$
Since LHS = RHS ($159 = 159$), the equation $a - (-b) = a + b$ is verified for $a = 75$ and $b = 84$.
(iv) Given $a = 28$ and $b = 11$.
LHS $= a - (-b) = 28 - (-11)$
LHS $= 28 + 11 = 39$
RHS $= a + b = 28 + 11 = 39$
Since LHS = RHS ($39 = 39$), the equation $a - (-b) = a + b$ is verified for $a = 28$ and $b = 11$.
Question 9. Use the sign of >, < or = in the box to make the statements true.
(a) (– 8) + (– 4) ⬜ (–8) – (– 4)
(b) (– 3) + 7 – (19) ⬜ 15 – 8 + (– 9)
(c) 23 – 41 + 11 ⬜ 23 – 41 – 11
(d) 39 + (– 24) – (15) ⬜ 36 + (– 52) – (– 36)
(e) – 231 + 79 + 51 ⬜ –399 + 159 + 81
Answer:
To make the statements true, we need to evaluate the expressions on both the left-hand side (LHS) and the right-hand side (RHS) of the box and then compare the results.
(a) (– 8) + (– 4) ⬜ (–8) – (– 4)
Evaluating the LHS:
$ (– 8) + (– 4) = – 8 – 4 = -12$
Evaluating the RHS:
$ (– 8) – (– 4) = – 8 + 4 = -4$
Comparison:
Since $-12$ is less than $-4$, the correct sign is '<'.
(– 8) + (– 4) < (–8) – (– 4)
(b) (– 3) + 7 – (19) ⬜ 15 – 8 + (– 9)
Evaluating the LHS:
$ (– 3) + 7 – 19 = 4 – 19 = -15$
Evaluating the RHS:
$ 15 – 8 + (– 9) = 7 – 9 = -2$
Comparison:
Since $-15$ is less than $-2$, the correct sign is '<'.
(– 3) + 7 – (19) < 15 – 8 + (– 9)
(c) 23 – 41 + 11 ⬜ 23 – 41 – 11
Evaluating the LHS:
$ 23 – 41 + 11 = (23 + 11) – 41 = 34 – 41 = -7$
Evaluating the RHS:
$ 23 – 41 – 11 = 23 – (41 + 11) = 23 – 52 = -29$
Comparison:
Since $-7$ is greater than $-29$, the correct sign is '>'.
23 – 41 + 11 > 23 – 41 – 11
(d) 39 + (– 24) – (15) ⬜ 36 + (– 52) – (– 36)
Evaluating the LHS:
$ 39 + (– 24) – 15 = 39 – 24 – 15 = 15 – 15 = 0$
Evaluating the RHS:
$ 36 + (– 52) – (– 36) = 36 – 52 + 36 = (36 + 36) – 52 = 72 – 52 = 20$
Comparison:
Since $0$ is less than $20$, the correct sign is '<'.
39 + (– 24) – (15) < 36 + (– 52) – (– 36)
(e) – 231 + 79 + 51 ⬜ –399 + 159 + 81
Evaluating the LHS:
$ – 231 + 79 + 51 = – 231 + (79 + 51) = – 231 + 130 = -101$
Evaluating the RHS:
$ – 399 + 159 + 81 = – 399 + (159 + 81) = – 399 + 240 = -159$
Comparison:
Since $-101$ is greater than $-159$, the correct sign is '>'.
– 231 + 79 + 51 > –399 + 159 + 81
Question 10. A water tank has steps inside it. A monkey is sitting on the topmost step (i.e., the first step). The water level is at the ninth step.
(i) He jumps 3 steps down and then jumps back 2 steps up. In how many jumps will he reach the water level?
(ii) After drinking water, he wants to go back. For this, he jumps 4 steps up and then jumps back 2 steps down in every move. In how many jumps will he reach back the top step?
(iii) If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers, represent his moves in part (i) and (ii) by completing the following;
(a) – 3 + 2 – ... = – 8
(b) 4 – 2 + ... = 8.
In (a) the sum (– 8) represents going down by eight steps. So, what will the sum 8 in (b) represent?
Answer:
Let the steps be numbered $1, 2, 3, ..., 9$ from top (step $1$) to bottom (step $9$).
The monkey is initially at step $1$. The water level is at step $9$.
(i) The monkey jumps $3$ steps down and then $2$ steps up.
Starting position: Step $1$.
Jump 1: $1 \xrightarrow{+3} 4$ (down). Position is step $4$.
Jump 2: $4 \xrightarrow{-2} 2$ (up). Position is step $2$.
Jump 3: $2 \xrightarrow{+3} 5$ (down). Position is step $5$.
Jump 4: $5 \xrightarrow{-2} 3$ (up). Position is step $3$.
Jump 5: $3 \xrightarrow{+3} 6$ (down). Position is step $6$.
Jump 6: $6 \xrightarrow{-2} 4$ (up). Position is step $4$.
Jump 7: $4 \xrightarrow{+3} 7$ (down). Position is step $7$.
Jump 8: $7 \xrightarrow{-2} 5$ (up). Position is step $5$.
Jump 9: $5 \xrightarrow{+3} 8$ (down). Position is step $8$.
Jump 10: $8 \xrightarrow{-2} 6$ (up). Position is step $6$.
Jump 11: $6 \xrightarrow{+3} 9$ (down). Position is step $9$. The monkey reaches the water level.
The monkey reaches the water level in $11$ jumps.
(ii) After drinking water, the monkey is at step $9$. He wants to go back to the top step ($1$).
He jumps $4$ steps up and then $2$ steps down.
Starting position: Step $9$.
Jump 1: $9 \xrightarrow{-4} 5$ (up). Position is step $5$.
Jump 2: $5 \xrightarrow{+2} 7$ (down). Position is step $7$.
Jump 3: $7 \xrightarrow{-4} 3$ (up). Position is step $3$.
Jump 4: $3 \xrightarrow{+2} 5$ (down). Position is step $5$.
Jump 5: $5 \xrightarrow{-4} 1$ (up). Position is step $1$. The monkey reaches the top step.
The monkey reaches back the top step in $5$ jumps.
(iii) Number of steps moved down is represented by negative integers, and the number of steps moved up by positive integers.
(a) This part represents the moves in part (i). The net displacement from step $1$ to step $9$ is $8$ steps downwards, represented by $-8$.
The sequence of moves is $-3$ (down $3$), $+2$ (up $2$). This repeats until the monkey reaches step $9$.
The sum represents the total change in position from the start (step $1$).
$-3$ (Jump 1, pos 4, displacement -3 from start)
$-3 + 2 = -1$ (Jump 2, pos 2, displacement -1 from start)
$-1 - 3 = -4$ (Jump 3, pos 5, displacement -4 from start)
$-4 + 2 = -2$ (Jump 4, pos 3, displacement -2 from start)
$-2 - 3 = -5$ (Jump 5, pos 6, displacement -5 from start)
$-5 + 2 = -3$ (Jump 6, pos 4, displacement -3 from start)
$-3 - 3 = -6$ (Jump 7, pos 7, displacement -6 from start)
$-6 + 2 = -4$ (Jump 8, pos 5, displacement -4 from start)
$-4 - 3 = -7$ (Jump 9, pos 8, displacement -7 from start)
$-7 + 2 = -5$ (Jump 10, pos 6, displacement -5 from start)
$-5 - 3 = -8$ (Jump 11, pos 9, displacement -8 from start)
Completing the sum: $-3 + 2 - 3 + 2 - 3 + 2 - 3 + 2 - 3 + 2 - 3 \ $$ = -8$.
(b) This part represents the moves in part (ii). The net displacement from step $9$ to step $1$ is $8$ steps upwards, represented by $8$.
The sequence of moves is $+4$ (up $4$), $-2$ (down $2$). This repeats until the monkey reaches step $1$.
The sum represents the total change in position from the start (step $9$).
$+4$ (Jump 1, pos 5, displacement +4 from start)
$+4 - 2 = +2$ (Jump 2, pos 7, displacement +2 from start)
$+2 + 4 = +6$ (Jump 3, pos 3, displacement +6 from start)
$+6 - 2 = +4$ (Jump 4, pos 5, displacement +4 from start)
$+4 + 4 = +8$ (Jump 5, pos 1, displacement +8 from start)
Completing the sum: $4 - 2 + 4 - 2 + 4 = 8$.
In (a) the sum ($-8$) represents going down by eight steps (from step $1$ to step $9$).
So, the sum $8$ in (b) represents going up by eight steps (from step $9$ to step $1$).
Example 1 (Before Exercise 1.2)
Example 1 Write down a pair of integers whose
(a) sum is –3
(b) difference is –5
(c) difference is 2
(d) sum is 0
Answer:
Here are some pairs of integers satisfying the given conditions. Note that there can be many other possible pairs.
(a) sum is –3
Let the two integers be $-1$ and $-2$.
$(-1) + (-2) = -3$
Another pair could be $-5$ and $2$.
$(-5) + 2 = -3$
A pair of integers whose sum is $-3$ is $\textbf{-1 and -2}$.
(b) difference is –5
Let the two integers be $1$ and $6$.
$1 - 6 = -5$
Another pair could be $-2$ and $3$.
$(-2) - 3 = -5$
A pair of integers whose difference is $-5$ is $\textbf{1 and 6}$.
(c) difference is 2
Let the two integers be $3$ and $1$.
$3 - 1 = 2$
Another pair could be $-1$ and $-3$.
$(-1) - (-3) = -1 + 3 = 2$
A pair of integers whose difference is $2$ is $\textbf{3 and 1}$.
(d) sum is 0
Let the two integers be $5$ and $-5$.
$5 + (-5) = 0$
Another pair could be $-10$ and $10$.
$(-10) + 10 = 0$
A pair of integers whose sum is $0$ is $\textbf{5 and -5}$.
Exercise 1.2
Question 1. Write down a pair of integers whose:
(a) sum is –7
(b) difference is –10
(c) sum is 0
Answer:
Here are possible pairs of integers for each part. Note that there are many other valid pairs.
(a) sum is –7
We need to find two integers, say $a$ and $b$, such that $a + b = -7$.
Let's choose $a = -3$. Then, $-3 + b = -7$. Solving for $b$, we get $b = -7 - (-3) = -7 + 3 = -4$.
So, a pair of integers is $-3$ and $-4$.
Check: $(-3) + (-4) = -7$.
Another possible pair could be $-10$ and $3$. Check: $(-10) + 3 = -7$.
A pair of integers whose sum is $-7$ is $\textbf{-3 and -4}$.
(b) difference is –10
We need to find two integers, say $a$ and $b$, such that $a - b = -10$.
Let's choose $a = 5$. Then, $5 - b = -10$. Solving for $b$, we get $-b = -10 - 5 = -15$, so $b = 15$.
So, a pair of integers is $5$ and $15$.
Check: $5 - 15 = -10$.
Another possible pair could be $-2$ and $8$. Check: $(-2) - 8 = -10$.
A pair of integers whose difference is $-10$ is $\textbf{5 and 15}$.
(c) sum is 0
We need to find two integers, say $a$ and $b$, such that $a + b = 0$. This means the two integers must be additive inverses of each other.
Let's choose $a = 5$. Then, $5 + b = 0$. Solving for $b$, we get $b = -5$.
So, a pair of integers is $5$ and $-5$.
Check: $5 + (-5) = 0$.
Any integer and its negative counterpart will work, e.g., $-12$ and $12$. Check: $(-12) + 12 = 0$.
A pair of integers whose sum is $0$ is $\textbf{5 and -5}$.
Question 2.
(a) Write a pair of negative integers whose difference gives 8.
(b) Write a negative integer and a positive integer whose sum is –5.
(c) Write a negative integer and a positive integer whose difference is –3.
Answer:
(a) Write a pair of negative integers whose difference gives 8.
Let's find a pair of negative integers, say `a` and `b`, such that $a - b = 8$.
We can choose a negative integer for `b` and then find `a`. Let's take $b = -2$.
$a - (-2) = 8$
$a + 2 = 8$
$a = 8 - 2 = 6$
Here, $a=6$ is a positive integer, so this pair (6, -2) is not valid. The first number must be less negative (closer to zero) than the second number.
Let's try another pair. Let the two integers be -2 and -10.
Their difference is:
$(–2) – (–10) = –2 + 10 = 8$
Thus, a pair of negative integers whose difference is 8 is (-2, -10).
(b) Write a negative integer and a positive integer whose sum is –5.
Let's find a negative integer and a positive integer whose sum is -5.
We can take the negative integer -10 and the positive integer 5.
Their sum is:
$(–10) + 5 = –5$
Thus, a valid pair is -10 (negative) and 5 (positive).
(c) Write a negative integer and a positive integer whose difference is –3.
Let's find a negative integer and a positive integer whose difference is -3. We need to be careful with the order of subtraction.
Case 1: (Negative Integer) - (Positive Integer) = -3
Let's take the negative integer -2 and the positive integer 1.
Their difference is:
$(–2) – 1 = –3$
This matches the condition. Thus, a valid pair is -2 (negative) and 1 (positive).
Question 3. In a quiz, team A scored – 40, 10, 0 and team B scored 10, 0, – 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
Answer:
Team A scored – 40, 10, and 0 in three successive rounds.
Total score of Team A = $(-40) + 10 + 0 = -30 + 0 = -30$.
Team B scored 10, 0, and – 40 in three successive rounds.
Total score of Team B = $10 + 0 + (-40) = 10 - 40 = -30$.
Comparing the scores, we see that the total score of Team A ($-30$) is equal to the total score of Team B ($-30$).
Therefore, neither team scored more; they both scored the same.
The scores of Team A and Team B involved the same set of numbers ($-40, 10, 0$) but in a different order of addition.
Team A: $(-40) + 10 + 0 = -30$
Team B: $10 + 0 + (-40) = -30$
Since changing the order of the addends did not change the sum, this demonstrates the commutative property of addition for integers.
Yes, we can say that we can add integers in any order.
Question 4. Fill in the blanks to make the following statements true:
(i) (–5) + (– 8) = (– 8) + (............)
(ii) –53 + ............ = –53
(iii) 17 + ............ = 0
(iv) [13 + (– 12)] + (............) = 13 + [(–12) + (–7)]
(v) (– 4) + [15 + (–3)] = [– 4 + 15] + .........…
Answer:
Let's fill in the blanks using the properties of integer addition.
(i) $ (–5) + (– 8) = (– 8) + (............) $
This statement follows the commutative property of addition, which states that the order of addends does not change the sum ($a + b = b + a$).
Comparing the given equation to the property, we have $a = -5$ and $b = -8$. The right side has $b$ first, so the blank must be $a$.
Therefore, the missing number is $-5$.
$(–5) + (– 8) = (– 8) + (\textbf{–5})$
(ii) $ –53 + ............ = –53 $
This statement follows the additive identity property, which states that when $0$ is added to any integer, the sum is the integer itself ($a + 0 = a$).
Comparing the given equation to the property, we have $a = -53$. The sum is still $-53$, so the number added must be $0$.
Therefore, the missing number is $0$.
–53 + 0 = –53
(iii) $ 17 + ............ = 0 $
This statement follows the additive inverse property, which states that the sum of an integer and its additive inverse (opposite) is $0$ ($a + (-a) = 0$).
Comparing the given equation, we have $a = 17$. To get a sum of $0$, we must add the additive inverse of $17$.
The additive inverse of $17$ is $-17$.
Therefore, the missing number is $-17$.
17 + (–17) = 0
(iv) $ [13 + (– 12)] + (............) = 13 + [(–12) + (–7)] $
This statement follows the associative property of addition, which states that the way integers are grouped in a sum does not change the sum ($(a + b) + c = a + (b + c)$).
Comparing the given equation to the property, we have $a = 13$, $b = -12$, and $c = -7$. The left side is grouped as $(a+b)+c$, and the right side is grouped as $a+(b+c)$.
The left side has $[13 + (-12)]$ grouped together, and the missing number is outside the brackets, corresponding to $c$. The right side has $13$ outside the brackets and $[(-12) + (-7)]$ grouped together, where $-12$ corresponds to $b$ and $-7$ corresponds to $c$.
Therefore, the missing number on the left side is $-7$.
$[13 + (– 12)] + (\textbf{–7}) = 13 + [(–12) + (–7)]$
(v) $ (– 4) + [15 + (–3)] = [– 4 + 15] + .........… $
This statement also follows the associative property of addition, $(a + b) + c = a + (b + c)$.
Comparing the given equation, the left side is grouped as $a + (b + c)$, where $a = -4$, $b = 15$, and $c = -3$. The right side is grouped as $(a + b) + c$, where $a = -4$ and $b = 15$ are grouped.
Therefore, the missing number on the right side corresponds to $c$, which is $-3$.
$(– 4) + [15 + (–3)] = [– 4 + 15] + \textbf{(–3)}$
Example 2 to 5 (Before Exercise 1.3)
Example 2 Find each of the following products:
(i) (–18) × (–10) × 9
(ii) (–20) × (–2) × (–5) × 7
(iii) (–1) × (–5) × (– 4) × (– 6)
Answer:
Let's find each of the following products:
(i) $ (–18) \times (–10) \times 9 $
First, multiply the first two integers: $ (-18) \times (-10) $. The product of two negative integers is a positive integer.
$ (-18) \times (-10) = 180 $
Now, multiply the result by the third integer: $ 180 \times 9 $.
$ 180 \times 9 = 1620 $
Alternatively, we can count the number of negative integers in the product. There are two negative integers (–18 and –10), which is an even number. Therefore, the product will be positive.
$ |{-18}| \times |{-10}| \times |9| = 18 \times 10 \times 9 = 180 \times 9 = 1620 $
Since the number of negative factors is even, the sign is positive.
The product is $1620$.
(ii) $ (–20) \times (–2) \times (–5) \times 7 $
Multiply step by step:
$ (-20) \times (-2) = 40 $ (Product of two negatives is positive)
$ 40 \times (-5) = -200 $ (Product of a positive and a negative is negative)
$ -200 \times 7 = -1400 $ (Product of a negative and a positive is negative)
Alternatively, count the number of negative integers. There are three negative integers (–20, –2, and –5), which is an odd number. Therefore, the product will be negative.
$ |{-20}| \times |{-2}| \times |{-5}| \times |7| = 20 \times 2 \times 5 \times 7 = 40 \times 5 \times 7 = 200 \times 7 \ $$ = 1400 $
Since the number of negative factors is odd, the sign is negative.
The product is $-1400$.
(iii) $ (–1) \times (–5) \times (– 4) \times (– 6) $
Multiply step by step:
$ (-1) \times (-5) = 5 $ (Product of two negatives is positive)
$ 5 \times (-4) = -20 $ (Product of a positive and a negative is negative)
$ -20 \times (-6) = 120 $ (Product of two negatives is positive)
Alternatively, count the number of negative integers. There are four negative integers (–1, –5, –4, and –6), which is an even number. Therefore, the product will be positive.
$ |{-1}| \times |{-5}| \times |{-4}| \times |{-6}| = 1 \times 5 \times 4 \times 6 = 5 \times 4 \times 6 = 20 \times 6 \ $$ = 120 $
Since the number of negative factors is even, the sign is positive.
The product is $120$.
Example 3 Verify (–30) × [13 + (–3)] = [(–30) × 13] + [(–30) × (–3)]
Answer:
We need to verify if the Left Hand Side (LHS) is equal to the Right Hand Side (RHS) of the given equation:
$ (–30) \times [13 + (–3)] = [(–30) \times 13] + [(–30) \times (–3)] $
Let's evaluate the Left Hand Side (LHS):
LHS = $ (–30) \times [13 + (–3)] $
First, calculate the expression inside the brackets:
$ 13 + (–3) = 13 - 3 = 10 $
Now, substitute this back into the LHS expression:
LHS = $ (–30) \times 10 $
The product of a negative integer and a positive integer is a negative integer. Multiply the absolute values: $30 \times 10 = 300$.
LHS = $ -300 $
Next, let's evaluate the Right Hand Side (RHS):
RHS = $ [(–30) \times 13] + [(–30) \times (–3)] $
First, calculate the first product inside the brackets:
$ (–30) \times 13 $
The product of a negative integer and a positive integer is a negative integer. Multiply the absolute values: $30 \times 13 = 390$.
$ (–30) \times 13 = -390 $
Second, calculate the second product inside the brackets:
$ (–30) \times (–3) $
The product of two negative integers is a positive integer. Multiply the absolute values: $30 \times 3 = 90$.
$ (–30) \times (–3) = 90 $
Now, add the two products:
RHS = $ (-390) + 90 $
Adding $90$ to $-390$ moves $90$ units towards the right on the number line from $-390$.
$ -390 + 90 = -300 $
RHS = $ -300 $
Comparing the LHS and RHS values:
LHS = $ -300 $
RHS = $ -300 $
Since LHS = RHS, the equation is verified.
This example demonstrates the distributive property of multiplication over addition for integers, which states that for any integers $a, b,$ and $c$, $a \times (b + c) = (a \times b) + (a \times c)$.
Example 4 In a class test containing 15 questions, 4 marks are given for every correct answer and (–2) marks are given for every incorrect answer.
(i) Gurpreet attempts all questions but only 9 of her answers are correct. What is her total score?
(ii) One of her friends gets only 5 answers correct. What will be her score?
Answer:
Given:
Total number of questions in the test = $15$.
Marks awarded for every correct answer = $4$.
Marks awarded for every incorrect answer = $-2$.
(i) Gurpreet attempts all 15 questions.
Number of correct answers = $9$.
Number of incorrect answers = Total questions - Number of correct answers = $15 - 9 = 6$.
Marks obtained for correct answers = Number of correct answers $\times$ Marks per correct answer
Marks obtained for correct answers = $9 \times 4 = 36$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks obtained for incorrect answers = $6 \times (-2) = -12$.
Total score of Gurpreet = Marks for correct answers + Marks for incorrect answers
Total score of Gurpreet = $36 + (-12) = 36 - 12 = 24$.
Gurpreet's total score is $24$.
(ii) One of her friends gets only 5 answers correct.
Number of correct answers = $5$.
Number of incorrect answers = Total questions - Number of correct answers = $15 - 5 = 10$.
Marks obtained for correct answers = Number of correct answers $\times$ Marks per correct answer
Marks obtained for correct answers = $5 \times 4 = 20$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks obtained for incorrect answers = $10 \times (-2) = -20$.
Total score of the friend = Marks for correct answers + Marks for incorrect answers
Total score of the friend = $20 + (-20) = 20 - 20 = 0$.
Her friend's score will be $0$.
Example 5 Suppose we represent the distance above the ground by a positive integer and that below the ground by a negative integer, then answer the following:
(i) An elevator descends into a mine shaft at the rate of 5 metre per minute. What will be its position after one hour?
(ii) If it begins to descend from 15 m above the ground, what will be its position after 45 minutes?
Answer:
We are representing the distance above the ground by a positive integer and the distance below the ground by a negative integer.
The elevator descends into a mine shaft at the rate of $5$ metre per minute. Since it is descending (going down, below ground), the rate of change in position is represented by a negative integer.
Rate of descent = $-5$ metre per minute.
(i) What will be its position after one hour?
Time taken = One hour.
Convert time into minutes: $1 \text{ hour} = 60 \text{ minutes}$.
The initial position of the elevator is not explicitly stated, but assuming it starts from ground level (step 0, or 0 m position), the displacement is calculated over time.
Displacement = Rate $\times$ Time
Displacement = $(-5 \text{ m/minute}) \times (60 \text{ minutes})$
Displacement = $-300$ metres.
Assuming the initial position is $0$ m (ground level), the final position is Initial position + Displacement.
Final position = $0 \text{ m} + (-300 \text{ m}) = -300 \text{ m}$.
The negative sign indicates the position is below the ground.
The position after one hour will be $300$ m below the ground.
(ii) If it begins to descend from 15 m above the ground, what will be its position after 45 minutes?
Initial position = 15 m above the ground.
Since distance above ground is positive, Initial position = $+15$ m.
Time taken = 45 minutes.
Rate of descent = $-5$ metre per minute.
Displacement = Rate $\times$ Time
Displacement = $(-5 \text{ m/minute}) \times (45 \text{ minutes})$
Displacement = $-225$ metres.
The final position is Initial position + Displacement.
Final position = $+15 \text{ m} + (-225 \text{ m})$
Final position = $15 - 225$ m
$15 - 225 = -210$ m.
The negative sign indicates the position is below the ground.
The position after 45 minutes will be $210$ m below the ground.
Exercise 1.3
Question 1. Find each of the following products:
(a) 3 × (–1)
(b) (–1) × 225
(c) (–21) × (–30)
(d) (–316) × (–1)
(e) (–15) × 0 × (–18)
(f) (–12) × (–11) × (10)
(g) 9 × (–3) × (– 6)
(h) (–18) × (–5) × (– 4)
(i) (–1) × (–2) × (–3) × 4
(j) (–3) × (–6) × (–2) × (–1)
Answer:
Let's find each of the following products:
(a) $ 3 \times (–1) $
When a positive integer is multiplied by a negative integer, the product is a negative integer.
$ 3 \times (–1) = -(3 \times 1) = -3 $
The product is $-3$.
(b) $ (–1) \times 225 $
When a negative integer is multiplied by a positive integer, the product is a negative integer.
$ (–1) \times 225 = -(1 \times 225) = -225 $
The product is $-225$.
(c) $ (–21) \times (–30) $
When a negative integer is multiplied by a negative integer, the product is a positive integer.
$ (–21) \times (–30) = +(21 \times 30) $
$ 21 \times 30 = 630 $
The product is $630$.
(d) $ (–316) \times (–1) $
When a negative integer is multiplied by a negative integer, the product is a positive integer.
$ (–316) \times (–1) = +(316 \times 1) = 316 $
The product is $316$.
(e) $ (–15) \times 0 \times (–18) $
When any integer is multiplied by zero, the product is always zero, regardless of other factors.
$ (–15) \times 0 = 0 $
Now, $ 0 \times (–18) = 0 $
The product is $0$.
(f) $ (–12) \times (–11) \times (10) $
First, multiply the first two negative integers:
$ (–12) \times (–11) = +(12 \times 11) = 132 $
Now, multiply the result by the positive integer:
$ 132 \times 10 = 1320 $
Alternatively, count the number of negative factors: 2 (which is even). The product is positive. $|-12| \times |-11| \times |10| \ $$ = 12 \times 11 \times 10 \ $$ = 132 \times 10 \ $$ = 1320$.
The product is $1320$.
(g) $ 9 \times (–3) \times (– 6) $
Multiply from left to right:
$ 9 \times (–3) = -27 $ (Positive $\times$ Negative = Negative)
Now, $ (-27) \times (–6) = +(27 \times 6) $ (Negative $\times$ Negative = Positive)
$ 27 \times 6 = 162 $
Alternatively, count the number of negative factors: 2 (which is even). The product is positive. $|9| \times |-3| \times |-6| = 9 \times 3 \times 6 = 27 \times 6 = 162$.
The product is $162$.
(h) $ (–18) \times (–5) \times (– 4) $
Multiply from left to right:
$ (–18) \times (–5) = +(18 \times 5) = 90 $ (Negative $\times$ Negative = Positive)
Now, $ 90 \times (–4) = -(90 \times 4) $ (Positive $\times$ Negative = Negative)
$ 90 \times 4 = 360 $
The product is $-360$.
Alternatively, count the number of negative factors: 3 (which is odd). The product is negative. $|-18| \times |-5| \times |-4| = 18 \times 5 \times 4 = 90 \times 4 = 360$. Since the number of negative factors is odd, the sign is negative.
The product is $-360$.
(i) $ (–1) \times (–2) \times (–3) \times 4 $
Multiply from left to right:
$ (–1) \times (–2) = 2 $ (Negative $\times$ Negative = Positive)
$ 2 \times (–3) = -6 $ (Positive $\times$ Negative = Negative)
$ (-6) \times 4 = -24 $ (Negative $\times$ Positive = Negative)
Alternatively, count the number of negative factors: 3 (which is odd). The product is negative. $|-1| \times |-2| \times |-3| \times |4| \ $$ = 1 \times 2 \times 3 \times 4 \ $$ = 2 \times 3 \times 4 = 6 \times 4 = 24$. Since the number of negative factors is odd, the sign is negative.
The product is $-24$.
(j) $ (–3) \times (–6) \times (–2) \times (–1) $
Multiply from left to right:
$ (–3) \times (–6) = 18 $ (Negative $\times$ Negative = Positive)
$ 18 \times (–2) = -36 $ (Positive $\times$ Negative = Negative)
$ (-36) \times (–1) = 36 $ (Negative $\times$ Negative = Positive)
Alternatively, count the number of negative factors: 4 (which is even). The product is positive. $|-3| \times |-6| \times |-2| \times |-1| = 3 \times 6 \times 2 \times 1 \ $$ = 18 \times 2 \times 1 = 36 \times 1 = 36$. Since the number of negative factors is even, the sign is positive.
The product is $36$.
Question 2. Verify the following:
(a) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]
(b) (–21) × [(– 4) + (– 6)] = [(–21) × (– 4)] + [(–21) × (– 6)]
Answer:
We need to verify if the Left Hand Side (LHS) is equal to the Right Hand Side (RHS) for each equation.
(a) Verify $ 18 \times [7 + (–3)] = [18 \times 7] + [18 \times (–3)] $
This equation illustrates the distributive property of multiplication over addition: $a \times (b + c) = (a \times b) + (a \times c)$, where $a=18$, $b=7$, and $c=-3$.
Let's evaluate the Left Hand Side (LHS):
LHS = $ 18 \times [7 + (–3)] $
First, calculate the expression inside the brackets:
$ 7 + (–3) = 7 - 3 = 4 $
Now, substitute this back into the LHS expression:
LHS = $ 18 \times 4 = 72 $
Let's evaluate the Right Hand Side (RHS):
RHS = $ [18 \times 7] + [18 \times (–3)] $
Calculate the first product:
$ 18 \times 7 = 126 $
Calculate the second product:
$ 18 \times (–3) = -(18 \times 3) = -54 $
Now, add the two products:
RHS = $ 126 + (–54) = 126 - 54 = 72 $
Comparing the LHS and RHS values:
LHS = $ 72 $
RHS = $ 72 $
Since LHS = RHS, the statement is verified.
(b) Verify $ (–21) \times [(– 4) + (– 6)] = [(–21) \times (– 4)] + [(–21) \times (– 6)] $
This equation also illustrates the distributive property of multiplication over addition: $a \times (b + c) = (a \times b) + (a \times c)$, where $a=-21$, $b=-4$, and $c=-6$.
Let's evaluate the Left Hand Side (LHS):
LHS = $ (–21) \times [(– 4) + (– 6)] $
First, calculate the expression inside the brackets:
$ (– 4) + (– 6) = -4 - 6 = -10 $
Now, substitute this back into the LHS expression:
LHS = $ (–21) \times (–10) $
The product of two negative integers is positive:
$ (–21) \times (–10) = +(21 \times 10) = 210 $
LHS = $ 210 $
Let's evaluate the Right Hand Side (RHS):
RHS = $ [(–21) \times (– 4)] + [(–21) \times (– 6)] $
Calculate the first product:
$ (–21) \times (– 4) = +(21 \times 4) = 84 $ (Product of two negatives is positive)
Calculate the second product:
$ (–21) \times (– 6) = +(21 \times 6) = 126 $ (Product of two negatives is positive)
Now, add the two products:
RHS = $ 84 + 126 $
$ 84 + 126 = 210 $
RHS = $ 210 $
Comparing the LHS and RHS values:
LHS = $ 210 $
RHS = $ 210 $
Since LHS = RHS, the statement is verified.
Question 3.
(i) For any integer a, what is (–1) × a equal to?
(ii) Determine the integer whose product with (–1) is
(a) –22
(b) 37
(c) 0
Answer:
Let's answer the given questions.
(i) For any integer a, what is (–1) × a equal to?
When an integer $a$ is multiplied by $-1$, the result is the additive inverse (or opposite) of $a$.
$(-1) \times a = -a$
For example, if $a = 5$, $(-1) \times 5 = -5$. If $a = -7$, $(-1) \times (-7) = 7$.
So, for any integer $a$, $(-1) \times a$ is equal to $-a$.
(ii) Determine the integer whose product with (–1) is:
Let the integer be $x$. We are given that $x \times (-1)$ equals a certain value. We need to find $x$.
The equation is $x \times (-1) = \text{given value}$.
Since $x \times (-1) = -x$, the equation becomes $-x = \text{given value}$.
To find $x$, we take the additive inverse of the given value, i.e., $x = -(\text{given value})$.
Let's solve for each case:
(a) –22
We need to find an integer $x$ such that $x \times (-1) = -22$.
This means $-x = -22$.
Multiplying both sides by $-1$, we get $x = -(-22) = 22$.
The integer is $22$.
Check: $22 \times (-1) = -22$.
(b) 37
We need to find an integer $x$ such that $x \times (-1) = 37$.
This means $-x = 37$.
Multiplying both sides by $-1$, we get $x = -(37) = -37$.
The integer is $-37$.
Check: $(-37) \times (-1) = 37$.
(c) 0
We need to find an integer $x$ such that $x \times (-1) = 0$.
This means $-x = 0$.
The only number whose additive inverse is $0$ is $0$ itself. $x = -(0) = 0$.
The integer is $0$.
Check: $0 \times (-1) = 0$.
Question 4. Starting from (–1) × 5, write various products showing some pattern to show (–1) × (–1) = 1.
Answer:
We can write a series of products starting from $(-1) \times 5$ by decreasing the second integer by $1$ in each step and observe the pattern in the results.
Let's start with the given product:
$(-1) \times 5 = -5$
Now, decrease the second factor by $1$ and find the product:
$(-1) \times 4 = -4$ (The result $-4$ is $1$ more than $-5$)
$(-1) \times 3 = -3$ (The result $-3$ is $1$ more than $-4$)
$(-1) \times 2 = -2$ (The result $-2$ is $1$ more than $-3$)
$(-1) \times 1 = -1$ (The result $-1$ is $1$ more than $-2$)
$(-1) \times 0 = 0$ (The result $0$ is $1$ more than $-1$)
Following this pattern, when we multiply $(-1)$ by the next integer in the decreasing sequence, which is $-1$, the result should be $1$ more than the previous result ($0$).
$(-1) \times (-1) = 0 + 1 = 1$
The pattern shows that as we decrease the integer multiplied by $-1$ by one, the product increases by one.
Starting from $(-1) \times 5 = -5$, and repeatedly adding $1$ for each step down in the second factor:
$-5 \xrightarrow{+1} -4 \xrightarrow{+1} -3 \xrightarrow{+1} -2 \xrightarrow{+1} -1 \xrightarrow{+1} 0 \xrightarrow{+1} 1$
This pattern leads to the conclusion that $(-1) \times (-1)$ should be $1$ more than $(-1) \times 0$, which is $0 + 1 = 1$.
Thus, the pattern demonstrates that $(-1) \times (-1) = 1$.
Question 5. Find the product, using suitable properties:
(a) 26 × (– 48) + (– 48) × (–36)
(b) 8 × 53 × (–125)
(c) 15 × (–25) × (– 4) × (–10)
(d) (– 41) × 102
(e) 625 × (–35) + (– 625) × 65
(f) 7 × (50 – 2)
(g) (–17) × (–29)
(h) (–57) × (–19) + 57
Answer:
Let's find the product for each expression using suitable properties of integers.
(a) $ 26 \times (– 48) + (– 48) \times (–36) $
This expression is in the form $a \times b + a \times c$. We can use the distributive property of multiplication over addition in reverse: $a \times (b + c) = a \times b + a \times c$.
Here, $a = –48$, $b = 26$, and $c = –36$.
$ 26 \times (– 48) + (– 48) \times (–36) = (– 48) \times [26 + (–36)] $
First, calculate the sum inside the brackets:
$ 26 + (–36) = 26 - 36 = -10 $
Now, substitute this value back into the expression:
$ (– 48) \times (-10) $
The product of two negative integers is a positive integer.
$ (– 48) \times (-10) = 480 $
The product is $480$.
(b) $ 8 \times 53 \times (–125) $
This expression involves multiplication of three integers. We can use the commutative property of multiplication ($a \times b = b \times a$) and the associative property of multiplication ($(a \times b) \times c = a \times (b \times c)$) to rearrange and group the factors for easier calculation. It is easier to multiply $8$ and $-125$ first.
$ 8 \times 53 \times (–125) = 53 \times [8 \times (–125)] $
First, calculate the product inside the brackets:
$ 8 \times (–125) = -(8 \times 125) = -1000 $
Now, substitute this value back into the expression:
$ 53 \times (-1000) $
The product of a positive integer and a negative integer is a negative integer.
$ 53 \times (-1000) = -53000 $
The product is $-53000$.
(c) $ 15 \times (–25) \times (– 4) \times (–10) $
This involves multiplication of four integers. We can use the associative and commutative properties to group convenient factors.
$ 15 \times (–25) \times (– 4) \times (–10) = 15 \times [(-25) \times (-4)] \times (-10) $
First, calculate the product inside the brackets:
$ (-25) \times (-4) = 100 $ (Product of two negatives is positive)
Now, substitute this value back and continue multiplying:
$ 15 \times 100 \times (–10) $
Multiply $15 \times 100$:
$ 15 \times 100 = 1500 $
Now, multiply the result by $-10$:
$ 1500 \times (–10) = -15000 $ (Product of a positive and a negative is negative)
Alternatively, count the number of negative factors: 3 (odd), so the result is negative. $ |15| \times |–25| \times |– 4| \times |–10| \ $$ = 15 \times 25 \times 4 \times 10 \ $$ = 15 \times (25 \times 4) \times 10 \ $$ = 15 \times 100 \times 10 \ $$ = 15000$. With the negative sign, the product is $-15000$.
The product is $-15000$.
(d) $ (– 41) \times 102 $
We can use the distributive property of multiplication over addition by writing $102$ as a sum, for example $100 + 2$.
$ (– 41) \times 102 = (– 41) \times (100 + 2) $
Apply the distributive property $a \times (b + c) = (a \times b) + (a \times c)$ with $a = -41$, $b = 100$, and $c = 2$:
$ (– 41) \times (100 + 2) = (– 41 \times 100) + (– 41 \times 2) $
Calculate the products:
$ (– 41 \times 100) = -4100 $
$ (– 41 \times 2) = -82 $
Now, add the results:
$ -4100 + (-82) = -4100 - 82 = -4182 $
The product is $-4182$.
(e) $ 625 \times (–35) + (– 625) \times 65 $
This expression is in the form $a \times b + c \times d$. Notice that $c = -625$, which is the additive inverse of $625$. We can rewrite the second term: $ (– 625) \times 65 = 625 \times (-65) $. Now the expression is in the form $a \times b + a \times c$, where $a=625$, $b=-35$, and $c=-65$. Use the distributive property in reverse.
$ 625 \times (–35) + (– 625) \times 65 = 625 \times (–35) + 625 \times (–65) $
$ = 625 \times [(-35) + (-65)] $
First, calculate the sum inside the brackets:
$ (-35) + (-65) = -35 - 65 = -100 $
Now, substitute this value back into the expression:
$ 625 \times (-100) $
The product of a positive integer and a negative integer is a negative integer.
$ 625 \times (-100) = -62500 $
The product is $-62500$.
(f) $ 7 \times (50 – 2) $
This expression directly uses the distributive property of multiplication over subtraction: $a \times (b - c) = a \times b - a \times c$, with $a=7$, $b=50$, and $c=2$. Alternatively, we can perform the subtraction inside the brackets first.
Method 1 (Using Distributive Property):
$ 7 \times (50 – 2) = (7 \times 50) - (7 \times 2) $
$ 7 \times 50 = 350 $
$ 7 \times 2 = 14 $
Now, subtract the results:
$ 350 - 14 = 336 $
Method 2 (Calculating inside brackets first):
$ 7 \times (50 – 2) = 7 \times (48) $
$ 7 \times 48 = 336 $
Both methods give the same result.
The product is $336$.
(g) $ (–17) \times (–29) $
The product of two negative integers is a positive integer. We can multiply the absolute values: $ 17 \times 29 $. To use properties, we can write $-29$ as $ (-30) + 1 $ and use the distributive property.
$ (–17) \times (–29) = (–17) \times [(-30) + 1] $
Apply the distributive property $a \times (b + c) = (a \times b) + (a \times c)$ with $a = -17$, $b = -30$, and $c = 1$:
$ = (–17 \times –30) + (–17 \times 1) $
Calculate the products:
$ (–17 \times –30) = 510 $ (Product of two negatives is positive)
$ (–17 \times 1) = -17 $
Now, add the results:
$ 510 + (-17) = 510 - 17 = 493 $
Alternatively, direct multiplication $17 \times 29 = 493$. Since both factors are negative, the result is positive $493$.
The product is $493$.
(h) $ (–57) \times (–19) + 57 $
This expression can be rewritten to use the distributive property. Note that $57 = 57 \times 1$. Also, $–57 = -1 \times 57$.
$ (–57) \times (–19) + 57 = (-1 \times 57) \times (-19) + 57 \times 1 $
Using associative property on the first term: $ (-1 \times 57) \times (-19) = 57 \times (-1 \times -19) = 57 \times 19 $.
So the expression becomes: $ 57 \times 19 + 57 \times 1 $
Now, use the distributive property in reverse: $a \times b + a \times c = a \times (b + c)$, with $a = 57$, $b = 19$, and $c = 1$.
$ 57 \times 19 + 57 \times 1 = 57 \times (19 + 1) $
Calculate the sum inside the brackets:
$ 19 + 1 = 20 $
Now, substitute this value back into the expression:
$ 57 \times 20 $
$ 57 \times 20 = 1140 $
The product is $1140$.
Question 6. A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5°C every hour. What will be the room temperature 10 hours after the process begins?
Answer:
Given:
Initial room temperature = $40^\circ \text{C}$.
Rate at which temperature is lowered = $5^\circ \text{C}$ every hour.
Since the temperature is being lowered, the change in temperature per hour is represented by a negative integer: $-5^\circ \text{C}$.
Time duration = $10$ hours.
We need to find the room temperature after $10$ hours.
The total change in temperature after $10$ hours is the rate of change per hour multiplied by the number of hours.
Total change in temperature = Rate of change $\times$ Time
Total change in temperature = $(-5^\circ \text{C/hour}) \times (10 \text{ hours})$
Total change in temperature = $-50^\circ \text{C}$.
The final room temperature will be the initial temperature plus the total change in temperature.
Final temperature = Initial temperature + Total change in temperature
Final temperature = $40^\circ \text{C} + (-50^\circ \text{C})$
Final temperature = $40 - 50$
Final temperature = $-10^\circ \text{C}$.
The room temperature $10$ hours after the process begins will be $-10^\circ \text{C}$.
Question 7. In a class test containing 10 questions, 5 marks are awarded for every correct answer and (–2) marks are awarded for every incorrect answer and 0 for questions not attempted.
(i) Mohan gets four correct and six incorrect answers. What is his score?
(ii) Reshma gets five correct answers and five incorrect answers, what is her score?
(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
Answer:
Given marking scheme for the class test with $10$ questions:
Marks awarded for every correct answer = $5$ marks.
Marks awarded for every incorrect answer = $-2$ marks.
Marks awarded for questions not attempted = $0$ marks.
(i) Mohan's score:
Mohan gets four correct answers and six incorrect answers.
Number of correct answers = $4$.
Number of incorrect answers = $6$.
Total questions attempted by Mohan = Number of correct answers + Number of incorrect answers = $4 + 6 = 10$.
Since the total number of questions is $10$, Mohan attempted all questions. Number of questions not attempted = $10 - 10 = 0$.
Marks obtained for correct answers = Number of correct answers $\times$ Marks per correct answer
Marks obtained for correct answers = $4 \times 5 = 20$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks obtained for incorrect answers = $6 \times (-2) = -12$.
Marks obtained for not attempted questions = Number of not attempted questions $\times$ Marks per not attempted question
Marks obtained for not attempted questions = $0 \times 0 = 0$.
Mohan's total score = Marks for correct answers + Marks for incorrect answers + Marks for not attempted questions
Mohan's total score = $20 + (-12) + 0$
Mohan's total score = $20 - 12 = 8$.
Mohan's score is $8$.
(ii) Reshma's score:
Reshma gets five correct answers and five incorrect answers.
Number of correct answers = $5$.
Number of incorrect answers = $5$.
Total questions attempted by Reshma = Number of correct answers + Number of incorrect answers = $5 + 5 = 10$.
Since the total number of questions is $10$, Reshma attempted all questions. Number of questions not attempted = $10 - 10 = 0$.
Marks obtained for correct answers = Number of correct answers $\times$ Marks per correct answer
Marks obtained for correct answers = $5 \times 5 = 25$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks obtained for incorrect answers = $5 \times (-2) = -10$.
Marks obtained for not attempted questions = Number of not attempted questions $\times$ Marks per not attempted question
Marks obtained for not attempted questions = $0 \times 0 = 0$.
Reshma's total score = Marks for correct answers + Marks for incorrect answers + Marks for not attempted questions
Reshma's total score = $25 + (-10) + 0$
Reshma's total score = $25 - 10 = 15$.
Reshma's score is $15$.
(iii) Heena's score:
Heena gets two correct and five incorrect answers out of seven questions she attempts.
Number of correct answers = $2$.
Number of incorrect answers = $5$.
Total questions attempted by Heena = $7$.
Total number of questions in the test = $10$.
Number of questions not attempted = Total questions - Total questions attempted = $10 - 7 = 3$.
Marks obtained for correct answers = Number of correct answers $\times$ Marks per correct answer
Marks obtained for correct answers = $2 \times 5 = 10$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks obtained for incorrect answers = $5 \times (-2) = -10$.
Marks obtained for not attempted questions = Number of not attempted questions $\times$ Marks per not attempted question
Marks obtained for not attempted questions = $3 \times 0 = 0$.
Heena's total score = Marks for correct answers + Marks for incorrect answers + Marks for not attempted questions
Heena's total score = $10 + (-10) + 0$
Heena's total score = $10 - 10 + 0 = 0$.
Heena's score is $0$.
Question 8. A cement company earns a profit of ₹ 8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold.
(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?
(b) What is the number of white cement bags it must sell to have neither profit nor loss, if the number of grey bags sold is 6,400 bags.
Answer:
Given:
Profit per bag of white cement sold = $\textsf{₹} \, 8$.
Loss per bag of grey cement sold = $\textsf{₹} \, 5$. (This can be represented as a profit of $-\textsf{₹} \, 5$ per bag).
(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month.
Number of white cement bags sold = $3000$.
Number of grey cement bags sold = $5000$.
Profit from selling white cement bags = Number of white bags $\times$ Profit per white bag
Profit from selling white cement bags = $3000 \times \textsf{₹} \, 8 = \textsf{₹} \, 24000$.
Loss from selling grey cement bags = Number of grey bags $\times$ Loss per grey bag
Loss from selling grey cement bags = $5000 \times \textsf{₹} \, 5 = \textsf{₹} \, 25000$.
Alternatively, Profit from selling grey cement bags = $5000 \times (-\textsf{₹} \, 5) = -\textsf{₹} \, 25000$.
Total profit or loss = Profit from white cement + Profit from grey cement (or - Loss from grey cement)
Total profit or loss = $\textsf{₹} \, 24000 + (-\textsf{₹} \, 25000)$
Total profit or loss = $\textsf{₹} \, (24000 - 25000)$
Total profit or loss = $-\textsf{₹} \, 1000$.
Since the total is negative, it represents a loss.
The company has a loss of $\textsf{₹} \, 1000$.
(b) The company has neither profit nor loss, and the number of grey bags sold is 6,400.
Let the number of white cement bags it must sell be $x$.
Number of grey cement bags sold = $6400$.
For neither profit nor loss, the total profit must be equal to the total loss (or the sum of profit and loss must be zero).
Profit from selling white cement bags = Number of white bags $\times$ Profit per white bag
Profit from selling white cement bags = $x \times \textsf{₹} \, 8 = \textsf{₹} \, 8x$.
Loss from selling grey cement bags = Number of grey bags $\times$ Loss per grey bag
Loss from selling grey cement bags = $6400 \times \textsf{₹} \, 5 = \textsf{₹} \, 32000$.
Condition for neither profit nor loss:
Total Profit = Total Loss
$8x = 32000$
To find $x$, divide both sides by $8$:
$\frac{\cancel{8}x}{\cancel{8}} = \frac{32000}{8}$
$x = 4000$
The company must sell $4000$ bags of white cement to have neither profit nor loss if 6,400 bags of grey cement are sold.
The number of white cement bags it must sell is $4000$ bags.
Question 9. Replace the blank with an integer to make it a true statement.
(a) (–3) × _____ = 27
(b) 5 × _____ = –35
(c) _____ × (– 8) = –56
(d) _____ × (–12) = 132
Answer:
Let's replace the blank with an integer to make each statement true. Let the blank be represented by $x$ in each case.
(a) $ (–3) \times x = 27 $
To find the value of $x$, we need to divide the product ($27$) by the known factor ($-3$).
$ x = \frac{27}{-3} $
When dividing a positive integer by a negative integer, the result is a negative integer.
$ \frac{27}{3} = 9 $
So, $ x = -9 $.
Check: $ (–3) \times (–9) = 27 $ (Since negative $\times$ negative = positive, and $3 \times 9 = 27$). This is correct.
The blank should be –9.
(b) $ 5 \times x = –35 $
To find the value of $x$, we need to divide the product ($-35$) by the known factor ($5$).
$ x = \frac{-35}{5} $
When dividing a negative integer by a positive integer, the result is a negative integer.
$ \frac{35}{5} = 7 $
So, $ x = -7 $.
Check: $ 5 \times (–7) = -35 $ (Since positive $\times$ negative = negative, and $5 \times 7 = 35$). This is correct.
The blank should be –7.
(c) $ x \times (– 8) = –56 $
To find the value of $x$, we need to divide the product ($-56$) by the known factor ($-8$).
$ x = \frac{-56}{-8} $
When dividing a negative integer by a negative integer, the result is a positive integer.
$ \frac{56}{8} = 7 $
So, $ x = 7 $.
Check: $ 7 \times (– 8) = -56 $ (Since positive $\times$ negative = negative, and $7 \times 8 = 56$). This is correct.
The blank should be 7.
(d) $ x \times (–12) = 132 $
To find the value of $x$, we need to divide the product ($132$) by the known factor ($-12$).
$ x = \frac{132}{-12} $
When dividing a positive integer by a negative integer, the result is a negative integer.
$ \frac{132}{12} = 11 $
So, $ x = -11 $.
Check: $ (–11) \times (–12) = 132 $ (Since negative $\times$ negative = positive, and $11 \times 12 = 132$). This is correct.
The blank should be –11.
Example 6 & 7 (Before Exercise 1.4)
Example 6: In a test (+5) marks are given for every correct answer and (–2) marks are given for every incorrect answer.
(i) Radhika answered all the questions and scored 30 marks though she got 10 correct answers.
(ii) Jay also answered all the questions and scored (–12) marks though he got 4 correct answers. How many incorrect answers had they attempted?
Answer:
Given marking scheme for the class test:
Marks for every correct answer = $+5$
Marks for every incorrect answer = $-2$
Both students answered all the questions, meaning there are no unattempted questions.
(i) Radhika:
Radhika scored $30$ marks and got $10$ correct answers.
Let the number of incorrect answers Radhika attempted be $I_R$.
Marks obtained from correct answers = Number of correct answers $\times$ Marks per correct answer
Marks from correct answers = $10 \times 5 = 50$.
Marks obtained from incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks from incorrect answers = $I_R \times (-2) = -2I_R$.
Radhika's total score is the sum of marks from correct and incorrect answers:
$ \text{Marks from correct answers} + \text{Marks from incorrect answers} \ $$ = \text{Total score} $
$50 + (-2I_R) = 30$
$50 - 2I_R = 30$
Subtract $50$ from both sides:
$-2I_R = 30 - 50$
$-2I_R = -20$
Divide both sides by $-2$:
$\frac{\cancel{-2}I_R}{\cancel{-2}} = \frac{-20}{-2}$
$I_R = 10$
Radhika attempted $10$ incorrect answers.
(ii) Jay:
Jay scored $–12$ marks and got $4$ correct answers.
Let the number of incorrect answers Jay attempted be $I_J$.
Marks obtained from correct answers = Number of correct answers $\times$ Marks per correct answer
Marks from correct answers = $4 \times 5 = 20$.
Marks obtained from incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
Marks from incorrect answers = $I_J \times (-2) = -2I_J$.
Jay's total score is the sum of marks from correct and incorrect answers:
$ \text{Marks from correct answers} + \text{Marks from incorrect answers} \ $$ = \text{Total score} $
$20 + (-2I_J) = -12$
$20 - 2I_J = -12$
Subtract $20$ from both sides:
$-2I_J = -12 - 20$
$-2I_J = -32$
Divide both sides by $-2$:
$\frac{\cancel{-2}I_J}{\cancel{-2}} = \frac{-32}{-2}$
$I_J = 16$
Jay attempted $16$ incorrect answers.
Example 7: A shopkeeper earns a profit of ₹ 1 by selling one pen and incurs a loss of 40 paise per pencil while selling pencils of her old stock.
(i) In a particular month she incurs a loss of ₹ 5. In this period, she sold 45 pens. How many pencils did she sell in this period?
(ii) In the next month she earns neither profit nor loss. If she sold 70 pens, how many pencils did she sell?
Answer:
Given:
Profit earned by selling one pen = $\textsf{₹} \, 1$.
Loss incurred by selling one pencil = $40 \text{ paise}$.
We need to work with the same unit, so convert paise to Rupees.
$1 \text{ Rupee} = 100 \text{ paise}$.
$40 \text{ paise} = \frac{40}{100} \text{ Rupees} = \textsf{₹} \, 0.40$.
Loss per pencil = $\textsf{₹} \, 0.40$.
(i) In a particular month, she incurs a total loss of $\textsf{₹} \, 5$.
She sold $45$ pens in this period.
Let the number of pencils she sold be $x$.
Profit from selling pens = Number of pens sold $\times$ Profit per pen
Profit from selling pens = $45 \times \textsf{₹} \, 1 = \textsf{₹} \, 45$.
Loss from selling pencils = Number of pencils sold $\times$ Loss per pencil
Loss from selling pencils = $x \times \textsf{₹} \, 0.40 = \textsf{₹} \, 0.40x$.
Total loss incurred = $\textsf{₹} \, 5$.
The total loss is the difference between the total loss from pencils and the total profit from pens.
$ \text{Total Loss} = \text{Loss from pencils} - \text{Profit from pens} $
$ 5 = 0.40x - 45 $
Add $45$ to both sides of the equation:
$ 5 + 45 = 0.40x $
$ 50 = 0.40x $
To find $x$, divide both sides by $0.40$:
$ x = \frac{50}{0.40} $
We can write $0.40$ as $\frac{40}{100}$ or $\frac{4}{10}$ or $\frac{2}{5}$.
$ x = \frac{50}{\frac{4}{10}} = 50 \times \frac{10}{4} $
$ x = \frac{\cancel{50}^{25} \times 10}{\cancel{4}_{2}} = \frac{25 \times 10}{2} $
$ x = \frac{25 \times \cancel{10}^{5}}{\cancel{2}_{1}} = 25 \times 5 $
$ x = 125 $
She sold $125$ pencils in this period.
(ii) In the next month, she earns neither profit nor loss.
This means her total profit is equal to her total loss.
She sold $70$ pens.
Let the number of pencils she sold be $y$.
Profit from selling pens = Number of pens sold $\times$ Profit per pen
Profit from selling pens = $70 \times \textsf{₹} \, 1 = \textsf{₹} \, 70$.
Loss from selling pencils = Number of pencils sold $\times$ Loss per pencil
Loss from selling pencils = $y \times \textsf{₹} \, 0.40 = \textsf{₹} \, 0.40y$.
Condition for neither profit nor loss:
$ \text{Profit from pens} = \text{Loss from pencils} $
$ 70 = 0.40y $
To find $y$, divide both sides by $0.40$:
$ y = \frac{70}{0.40} $
Write $0.40$ as $\frac{4}{10}$.
$ y = \frac{70}{\frac{4}{10}} = 70 \times \frac{10}{4} $
$ y = \frac{\cancel{70}^{35} \times 10}{\cancel{4}_{2}} = \frac{35 \times 10}{2} $
$ y = \frac{35 \times \cancel{10}^{5}}{\cancel{2}_{1}} = 35 \times 5 $
$ y = 175 $
She sold $175$ pencils in the next month.
Exercise 1.4
Question 1. Evaluate each of the following:
(a) (–30) ÷ 10
(b) 50 ÷ (–5)
(c) (–36) ÷ (–9)
(d) (– 49) ÷ (49)
(e) 13 ÷ [(–2) + 1]
(f) 0 ÷ (–12)
(g) (–31) ÷ [(–30) + (–1)]
(h) [(–36) ÷ 12] ÷ 3
(i) [(– 6) + 5)] ÷ [(–2) + 1]
Answer:
Solution:
(a) $(–30) \div 10$
We need to divide $-30$ by $10$.
$\frac{-30}{10}$
When dividing a negative number by a positive number, the result is negative.
$\frac{-30}{10} = -3$
The value of $(–30) \div 10$ is $\mathbf{-3}$.
(b) $50 \div (–5)$
We need to divide $50$ by $-5$.
$\frac{50}{-5}$
When dividing a positive number by a negative number, the result is negative.
$\frac{50}{-5} = -10$
The value of $50 \div (–5)$ is $\mathbf{-10}$.
(c) $(–36) \div (–9)$
We need to divide $-36$ by $-9$.
$\frac{-36}{-9}$
When dividing a negative number by a negative number, the result is positive.
$\frac{-36}{-9} = 4$
The value of $(–36) \div (–9)$ is $\mathbf{4}$.
(d) $(– 49) \div (49)$
We need to divide $-49$ by $49$.
$\frac{-49}{49}$
When dividing a negative number by a positive number, the result is negative.
$\frac{-49}{49} = -1$
The value of $(– 49) \div (49)$ is $\mathbf{-1}$.
(e) $13 \div [(–2) + 1]$
First, evaluate the expression inside the brackets: $(–2) + 1$.
$(–2) + 1 = -1$
Now, perform the division: $13 \div (-1)$.
$\frac{13}{-1} = -13$
The value of $13 \div [(–2) + 1]$ is $\mathbf{-13}$.
(f) $0 \div (–12)$
We need to divide $0$ by $-12$.
$\frac{0}{-12}$
Dividing zero by any non-zero number results in zero.
$\frac{0}{-12} = 0$
The value of $0 \div (–12)$ is $\mathbf{0}$.
(g) $(–31) \div [(–30) + (–1)]$
First, evaluate the expression inside the brackets: $(–30) + (–1)$.
$(–30) + (–1) = -30 - 1 = -31$
Now, perform the division: $(-31) \div (-31)$.
$\frac{-31}{-31} = 1$
The value of $(–31) \div [(–30) + (–1)]$ is $\mathbf{1}$.
(h) $[(–36) \div 12] \div 3$
First, evaluate the expression inside the inner brackets: $(–36) \div 12$.
$(–36) \div 12 = -3$
Now, perform the outer division: $(-3) \div 3$.
$\frac{-3}{3} = -1$
The value of $[(–36) \div 12] \div 3$ is $\mathbf{-1}$.
(i) $[(– 6) + 5)] \div [(–2) + 1]$
First, evaluate the expression inside the first pair of brackets: $(– 6) + 5$.
$(– 6) + 5 = -1$
Next, evaluate the expression inside the second pair of brackets: $(–2) + 1$.
$(–2) + 1 = -1$
Now, perform the division of the results from the brackets: $(-1) \div (-1)$.
$\frac{-1}{-1} = 1$
The value of $[(– 6) + 5)] \div [(–2) + 1]$ is $\mathbf{1}$.
Question 2. Verify that a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c) for each of the following values of a, b and c.
(a) a = 12, b = – 4, c = 2
(b) a = (–10), b = 1, c = 1
Answer:
We need to verify that $a \div (b + c) \neq (a \div b) + (a \div c)$ for the given values of $a$, $b$, and $c$. We will evaluate both sides of the inequality separately for each case.
(a) Given $a = 12$, $b = -4$, $c = 2$.
Consider the Left Hand Side (LHS): $a \div (b + c)$
LHS = $12 \div (-4 + 2)$
First, calculate the sum inside the brackets:
$-4 + 2 = -2$
Now, perform the division:
$12 \div (-2) = \frac{12}{-2} = -6$
So, LHS = $-6$.
Now, consider the Right Hand Side (RHS): $(a \div b) + (a \div c)$
RHS = $(12 \div -4) + (12 \div 2)$
First, calculate the individual divisions:
$12 \div -4 = \frac{12}{-4} = -3$
$12 \div 2 = \frac{12}{2} = 6$
Now, perform the addition:
RHS = $-3 + 6 = 3$
So, RHS = $3$.
Comparing LHS and RHS:
LHS = $-6$ and RHS = $3$.
Since $-6 \neq 3$, we have $a \div (b + c) \neq (a \div b) + (a \div c)$.
Thus, the property is verified for $a = 12$, $b = -4$, $c = 2$.
(b) Given $a = -10$, $b = 1$, $c = 1$.
Consider the Left Hand Side (LHS): $a \div (b + c)$
LHS = $(-10) \div (1 + 1)$
First, calculate the sum inside the brackets:
$1 + 1 = 2$
Now, perform the division:
$(-10) \div 2 = \frac{-10}{2} = -5$
So, LHS = $-5$.
Now, consider the Right Hand Side (RHS): $(a \div b) + (a \div c)$
RHS = $(-10 \div 1) + (-10 \div 1)$
First, calculate the individual divisions:
$-10 \div 1 = \frac{-10}{1} = -10$
$-10 \div 1 = \frac{-10}{1} = -10$
Now, perform the addition:
RHS = $-10 + (-10) = -10 - 10 = -20$
So, RHS = $-20$.
Comparing LHS and RHS:
LHS = $-5$ and RHS = $-20$.
Since $-5 \neq -20$, we have $a \div (b + c) \neq (a \div b) + (a \div c)$.
Thus, the property is verified for $a = -10$, $b = 1$, $c = 1$.
In both cases (a) and (b), we have shown that $a \div (b + c)$ is not equal to $(a \div b) + (a \div c)$. Therefore, the given property $\mathbf{a \div (b + c) \neq (a \div b) + (a \div c)}$ is verified.
Question 3. Fill in the blanks:
(a) 369 ÷ _____ = 369
(b) (–75) ÷ _____ = –1
(c) (–206) ÷ _____ = 1
(d) – 87 ÷ _____ = 87
(e) _____ ÷ 1 = – 87
(f) _____ ÷ 48 = –1
(g) 20 ÷ _____ = –2
(h) _____ ÷ (4) = –3
Answer:
Solution:
(a) $369 \div$ _____ $= 369$
To get 369 when dividing 369, we must divide by 1.
$369 \div \mathbf{1} = 369$
The blank should be $\mathbf{1}$.
(b) $(–75) \div$ _____ $= –1$
Let the blank be $x$. The equation is $\frac{-75}{x} = -1$.
Multiplying both sides by $x$, we get $-75 = -x$.
Multiplying both sides by $-1$, we get $x = 75$.
$(–75) \div \mathbf{75} = –1$
The blank should be $\mathbf{75}$.
(c) $(–206) \div$ _____ $= 1$
Let the blank be $x$. The equation is $\frac{-206}{x} = 1$.
Multiplying both sides by $x$, we get $-206 = x$.
$(–206) \div \mathbf{(–206)} = 1$
The blank should be $\mathbf{-206}$.
(d) – 87 $\div$ _____ $= 87$
Let the blank be $x$. The equation is $\frac{-87}{x} = 87$.
Multiplying both sides by $x$, we get $-87 = 87x$.
Dividing both sides by 87, we get $x = \frac{-87}{87} = -1$.
$- 87 \div \mathbf{(–1)} = 87$
The blank should be $\mathbf{-1}$.
(e) _____ $\div 1 = – 87$
Let the blank be $x$. The equation is $\frac{x}{1} = -87$.
This simplifies to $x = -87$.
$\mathbf{(–87)} \div 1 = – 87$
The blank should be $\mathbf{-87}$.
(f) _____ $\div 48 = –1$
Let the blank be $x$. The equation is $\frac{x}{48} = -1$.
Multiplying both sides by 48, we get $x = -1 \times 48 = -48$.
$\mathbf{(–48)} \div 48 = –1$
The blank should be $\mathbf{-48}$.
(g) $20 \div$ _____ $= –2$
Let the blank be $x$. The equation is $\frac{20}{x} = -2$.
Multiplying both sides by $x$, we get $20 = -2x$.
Dividing both sides by $-2$, we get $x = \frac{20}{-2} = -10$.
$20 \div \mathbf{(–10)} = –2$
The blank should be $\mathbf{-10}$.
(h) _____ $\div (4) = –3$
Let the blank be $x$. The equation is $\frac{x}{4} = -3$.
Multiplying both sides by 4, we get $x = -3 \times 4 = -12$.
$\mathbf{(–12)} \div 4 = –3$
The blank should be $\mathbf{-12}$.
Question 4. Write five pairs of integers (a, b) such that a ÷ b = –3. One such pair is (6, –2) because 6 ÷ (–2) = (–3).
Answer:
Solution:
We are asked to find five pairs of integers $(a, b)$ such that the division of $a$ by $b$ results in $-3$.
This can be written as:
$a \div b = -3$
This is equivalent to $a = -3 \times b$.
We can choose different non-zero integer values for $b$ and then calculate the corresponding value for $a$.
Here are five such pairs:
1. If $b = 1$, then $a = -3 \times 1 = -3$. The pair is $\mathbf{(-3, 1)}$.
Check: $(-3) \div 1 = -3$.
2. If $b = 2$, then $a = -3 \times 2 = -6$. The pair is $\mathbf{(-6, 2)}$.
Check: $(-6) \div 2 = -3$.
3. If $b = -1$, then $a = -3 \times (-1) = 3$. The pair is $\mathbf{(3, -1)}$.
Check: $3 \div (-1) = -3$.
4. If $b = 3$, then $a = -3 \times 3 = -9$. The pair is $\mathbf{(-9, 3)}$.
Check: $(-9) \div 3 = -3$.
5. If $b = -4$, then $a = -3 \times (-4) = 12$. The pair is $\mathbf{(12, -4)}$.
Check: $12 \div (-4) = -3$.
Note that the example given, $(6, -2)$, also satisfies this condition: $6 \div (-2) = -3$. This corresponds to choosing $b = -2$, which gives $a = -3 \times (-2) = 6$.
So, five pairs of integers $(a, b)$ such that $a \div b = -3$ are $\mathbf{(-3, 1)}$, $\mathbf{(-6, 2)}$, $\mathbf{(3, -1)}$, $\mathbf{(-9, 3)}$, and $\mathbf{(12, -4)}$.
Question 5. The temperature at 12 noon was 10°C above zero. If it decreases at the rate of 2°C per hour until midnight, at what time would the temperature be 8°C below zero? What would be the temperature at mid-night?
Answer:
Solution:
Given:
Initial temperature at 12 noon = $10^\circ C$ above zero $= +10^\circ C$.
Rate of decrease of temperature = $2^\circ C$ per hour.
Part 1: Time when temperature is $8^\circ C$ below zero.
$8^\circ C$ below zero can be represented as $-8^\circ C$.
The temperature needs to drop from $10^\circ C$ to $-8^\circ C$.
Total temperature drop required = Initial temperature - Target temperature
Total temperature drop required = $10^\circ C - (-8^\circ C)$
Total temperature drop required = $10^\circ C + 8^\circ C = 18^\circ C$.
The temperature decreases at a rate of $2^\circ C$ per hour.
Time taken to reach the target temperature = $\frac{\text{Total temperature drop}}{\text{Rate of decrease}}$
Time taken = $\frac{18^\circ C}{2^\circ C / \text{hour}} = 9$ hours.
The temperature starts decreasing from 12 noon.
The time when the temperature would be $8^\circ C$ below zero is 9 hours after 12 noon.
12 noon + 9 hours = 9 p.m.
Thus, the temperature would be $8^\circ C$ below zero at 9 p.m.
Part 2: Temperature at midnight.
Midnight is 12 hours after 12 noon.
Duration from 12 noon to midnight = 12 hours.
Rate of decrease = $2^\circ C$ per hour.
Total decrease in temperature from 12 noon to midnight = Rate of decrease $\times$ Duration
Total decrease = $2^\circ C / \text{hour} \times 12$ hours = $24^\circ C$.
Temperature at midnight = Initial temperature at 12 noon - Total decrease.
Temperature at midnight = $10^\circ C - 24^\circ C = -14^\circ C$.
Thus, the temperature at midnight would be $\mathbf{-14^\circ C}$ (or $14^\circ C$ below zero).
Question 6. In a class test (+ 3) marks are given for every correct answer and (–2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores –5 marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?
Answer:
Given:
Marks for every correct answer = $+3$
Marks for every incorrect answer = $-2$
Marks for not attempting any question = $0$
(i) Radhika's case:
Given:
Radhika's total score = $20$
Number of correct answers by Radhika = $12$
To Find:
Number of questions attempted incorrectly by Radhika.
Solution:
Marks obtained by Radhika for $12$ correct answers = Number of correct answers $\times$ Marks per correct answer
$= 12 \times (+3) = 36$
Radhika's total score is the sum of marks from correct answers and marks from incorrect answers.
Marks obtained by Radhika for incorrect answers = Total score - Marks for correct answers
$= 20 - 36 = -16$
Let the number of incorrect answers be $n_i$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
$-16 = n_i \times (-2)$
To find $n_i$, we divide the total marks for incorrect answers by the marks per incorrect answer:
$n_i = \frac{-16}{-2}$
$n_i = 8$
So, Radhika attempted 8 questions incorrectly.
(ii) Mohini's case:
Given:
Mohini's total score = $-5$
Number of correct answers by Mohini = $7$
To Find:
Number of questions attempted incorrectly by Mohini.
Solution:
Marks obtained by Mohini for $7$ correct answers = Number of correct answers $\times$ Marks per correct answer
$= 7 \times (+3) = 21$
Mohini's total score is the sum of marks from correct answers and marks from incorrect answers.
Marks obtained by Mohini for incorrect answers = Total score - Marks for correct answers
$= -5 - 21 = -26$
Let the number of incorrect answers be $m_i$.
Marks obtained for incorrect answers = Number of incorrect answers $\times$ Marks per incorrect answer
$-26 = m_i \times (-2)$
To find $m_i$, we divide the total marks for incorrect answers by the marks per incorrect answer:
$m_i = \frac{-26}{-2}$
$m_i = 13$
So, Mohini attempted 13 questions incorrectly.
Question 7. An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.
Answer:
Given:
Starting position of the elevator = $10$ m above ground level. (We can represent ground level as $0$ m)
Starting position = $+10$ m.
Target position = $350$ m below ground level.
Target position = $-350$ m.
Rate of descent = $6$ m per minute.
To Find:
Time taken for the elevator to reach $-350$ m from $+10$ m.
Solution:
The total vertical distance the elevator needs to travel is the difference between the starting position and the target position.
Total distance to descend = Starting position - Target position
Total distance to descend = $(+10 \text{ m}) - (-350 \text{ m})$
Total distance to descend = $10 + 350$ m
Total distance to descend = $360$ m.
The elevator descends at a constant rate of $6$ m/min.
Time taken = $\frac{\text{Total distance to descend}}{\text{Rate of descent}}$
Time taken = $\frac{360 \text{ m}}{6 \text{ m/min}}$
Time taken = $\frac{360}{6}$ minutes
Time taken = $60$ minutes.
Since 60 minutes is equal to 1 hour, the time taken is 1 hour.
Thus, it will take 1 hour for the elevator to reach $-350$ m.

